You’re Not Cleared to Read This (Unless You Understand Lattices)
Imagine an intelligence analyst working at the NSA during the height of the Cold War. Let’s call her Alice. She has just completed a critical report by synthesizing satellite imagery and intercepted communications. The resulting document is classified at the highest level: (Top Secret, {CRYPTO, NATO}). This security label is more than just a stamp; it’s a precise declaration. It signifies not only the extreme sensitivity of the information (Top Secret) but also that it belongs to two distinct need-to-know compartments: CRYPTO, concerning cryptographic intelligence, and NATO, for information shared with allied nations.
Now, Alice faces a common but perilous task. She must prepare a briefing for Bob, a field agent involved in a joint operation. Bob’s clearance is (Secret, {NATO}). He is authorized to view Secret information and is a part of the NATO mission, but he is explicitly not cleared for the CRYPTO compartment. Alice cannot simply copy relevant paragraphs from her report into a new, lower-classification document for Bob. Doing so would be a catastrophic security breach, leaking highly sensitive cryptographic details to a channel not secured for them. This is the classic no write down problem, a cornerstone of information security.
How can a computer system be designed to enforce such a complex rule automatically, flawlessly, and with mathematical certainty? How can it prevent not just obvious copy-paste actions but also subtle, indirect leaks that a clever or careless user might create? This challenge reveals that true information security is not merely about passwords and firewalls that keep intruders out. That is only the first step. A far deeper problem lies in managing the legitimate actions of trusted insiders after they have logged in. The core issue is not just controlling access to information, but policing its flow. To solve this, computer scientists turned to a branch of pure mathematics that deals with the very essence of structure and order.
A Primer on Posets
Before building a fortress, one must understand the landscape. In the world of information, that landscape is defined by relationships. The mathematical tool for mapping these relationships is the partially ordered set, or poset.
To grasp what a partial order is, it helps to first consider its more familiar cousin, the total order. A total order is straightforward and linear; every element can be compared to every other element. The numbers on a number line are a total order (for any two different numbers, one is always greater than the other), as are words in a dictionary.
A partial order, however, describes a world rich with nuance and incomparability. Think of the prerequisite structure for university courses. Calculus I must be taken before Calculus II, creating an order. But Calculus I and Introduction to Philosophy have no required sequence; a student can take them in either order or at the same time. In the language of mathematics, these two courses are incomparable. Similarly, in building a house, the foundation must be laid before the walls are erected \(Foundation ≤ Walls\), but the electrical wiring and plumbing can often proceed in parallel. They are incomparable tasks within the overall project plan. These complex networks of dependencies, where some things are ordered and others are not, are partial orders.
This ability to handle incomparable elements is precisely what makes partial orders essential for modeling security. A simple, total order could represent the hierarchical military levels: \(Unclassified < Confidential < Secret < Top-Secret\). But this linear model breaks down when considering the need-to-know compartments from our opening scenario. Is the NATO compartment less than or greater than the CRYPTO compartment? Neither. They represent distinct, non-overlapping domains of information. An officer with a {NATO} clearance and another with a {CRYPTO} clearance have different, incomparable access rights. A partial order is the only mathematical structure that can faithfully represent this real-world complexity.
The Axioms of a Partial Order
For the technically inclined, a partially ordered set is formally defined as a set \(P\) combined with a binary relation, denoted by \(≤\), that satisfies three fundamental properties for any elements \(a\), \(b\), and \(c\) in \(P\):
-
Reflexivity: \(a≤a\):
Every element is related to itself. In our course analogy,Calculus Iis a prerequisite for itself in a trivial sense. -
Antisymmetry: \(If \ a≤b \ and \ b≤a, \ then \ a=b:\)
If two distinct elements are related in both directions, it creates a cycle, which is forbidden. IfCalculus Iis a prerequisite forPhilosophy,andPhilosophyis a prerequisite forCalculus I,then they must actually be the same course. -
Transitivity: \(If \ a≤b \ and \ b≤c, \ then \ a≤c:\)
The order is logical and chains together. IfCalculus Iis a prerequisite forCalculus II,andCalculus IIis a prerequisite forDifferential Equations,thenCalculus Iis implicitly a prerequisite forDifferential Equations.
What is a Lattice?
Posets provide a flexible way to map out relationships, but for building a robust security system, a bit more structure is needed. We need guarantees. A lattice is a special kind of well-behaved poset that guarantees we can always answer two critical questions for any pair of elements, \(a\) and \(b\):
-
What is the single, most specific element that is greater than or equal to both \(a\) and \(b\)? This is called the
Least Upper Bound (LUB), or thejoinof \(a\) and \(b\), written as \(a \vee b\). -
What is the single, most general element that is less than or equal to both \(a\) and \(b\)? This is the
Greatest Lower Bound (GLB), or themeetof \(a\) and \(b\), written as \(a \wedge b\).
The requirement that these join and meet elements must exist and be unique for every pair of elements is what gives a lattice its power and predictability.
The most intuitive example of a lattice is the power set (the set of all subsets) of a given set, ordered by the subset relation \((\subseteq)\). Consider the set \(\{X, Y\}\). Its power set is \(\{\}, \{X\}, \{Y\}, \{X, Y\}\). We can visualize this lattice using a Hasse diagram, a simple graph where nodes are the elements and an upward line from \(a\) to \(b\) means \(a\) is immediately below \(b\) in the order.
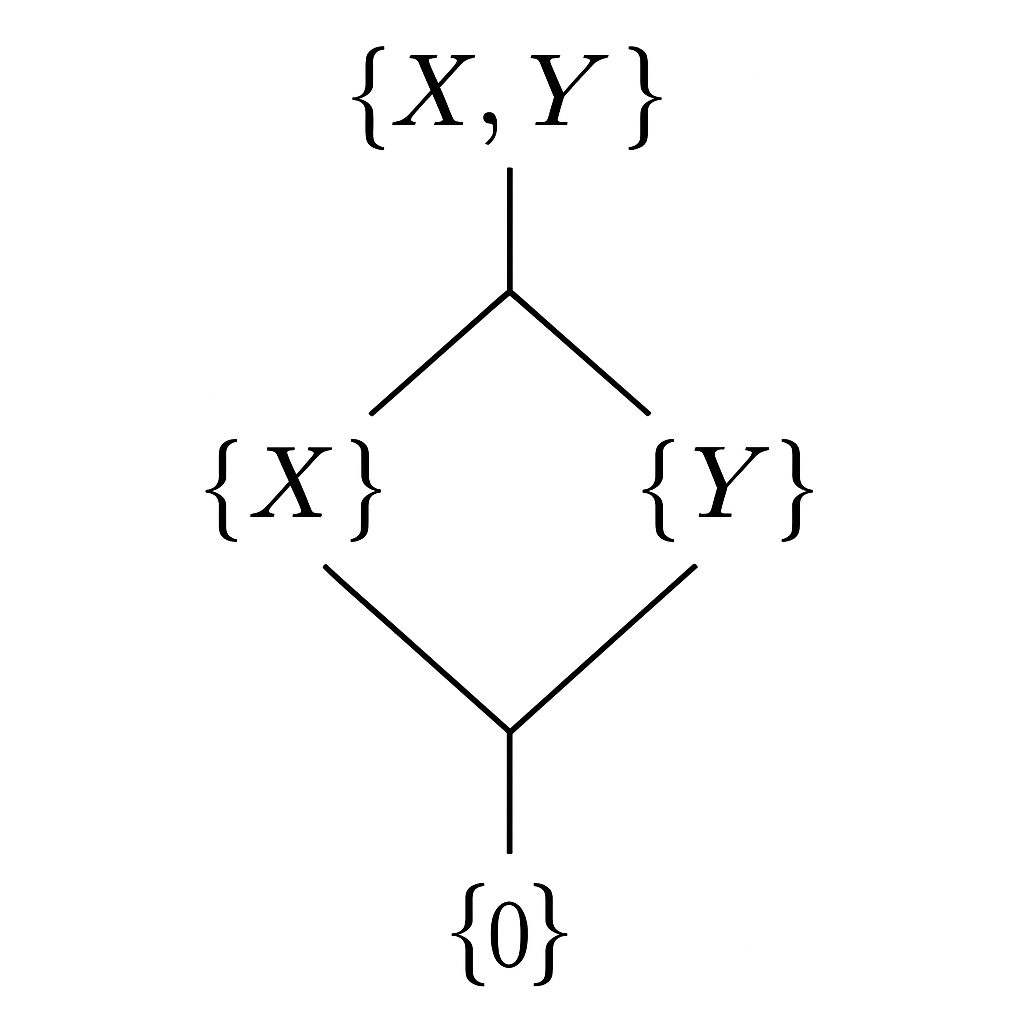
In this diagram, the bottom element is the empty set \(\{\}\), and the top is the full set \(\{X, Y\}\). Let’s find the join and meet of \(\{X\}\) and \(\{Y\}\):
-
Join: The upper bounds of \(\{X\}\) and \(\{Y\}\) are elements that contain both, in this case, only \(\{X, Y\}\). Since it’s the only one, it’s also the least upper bound. So, \(\{X\} \vee \{Y\} = \{X, Y\}\). This corresponds to the set union operation. -
Meet: The lower bounds are elements contained within both, in this case, only the empty set \(\{\}\), which is therefore the greatest lower bound. So, \(\{X\} \wedge \{Y\} = \{\}\). This corresponds to the set intersection operation.
This example reveals something profound. Lattices can be understood from two equivalent perspectives. The order-theoretic view sees a lattice as a static structure of relationships (a poset with LUB/GLB). The algebraic view sees it as a dynamic system with two operations (join and meet) that can be used for computation. This duality is what allows a lattice to serve as both an abstract model for a security policy and a concrete computational engine for enforcing it. The model describes the rules, and the algebra executes them.
Formal Definitions of a Lattice
A lattice can be defined in two equivalent ways:
-
Order-Theoretic Definition: A partially ordered set \((L,≤)\) is a lattice if, for every pair of elements \(a,b∈L\), both a least upper bound \((join, a∨b)\) and a greatest lower bound \((meet, a∧b)\) exist in \(L\). -
Algebraic Definition: A set \(L\) equipped with two binary operations, \(join (∨)\) and \(meet (∧)\), is a lattice if for all \(a,b,c∈L\), the following identities hold:-
Commutative Laws: \(a∨b=b∨a \hspace{0.5em} and \hspace{0.5em} a∧b=b∧a\). -
Associative Laws: \(a∨(b∨c)=(a∨b)∨c \hspace{0.4em} and \hspace{0.4em} a∧(b∧c)=(a∧b)∧c\). -
Absorption Laws: \(a∨(a∧b)=a \hspace{0.5em} and \hspace{0.5em} a∧(a∨b)=a\).
-
The absorption laws elegantly link the two operations and ensure that the algebraic structure corresponds to a valid partial order.
From Abstract Math to Concrete Security
The leap from abstract lattices to computer security happens when we assign specific meanings to the lattice’s components. This is the core of Lattice-Based Access Control (LBAC).
- The elements of the set become security labels.
- The partial order relation \(A≤B\) is reinterpreted as a
can-flow policy: Information is permitted to flow from an object with label A to an object with label B.
This framework was formally established by Dorothy Denning in her groundbreaking 1976 paper, A Lattice Model of Secure Information Flow. Denning demonstrated that any coherent set of security classifications naturally forms a lattice. The join operation becomes the fundamental rule for information aggregation: if a program combines data from a source with label A and another with label B, the resulting data must be protected by a new label that is at least as restrictive as both. The mathematically correct label for this new data is the join of the source labels, \(A∨B\). This prevents information from being laundered by mixing it with less sensitive data.
The most famous and influential application of this model is the Bell-LaPadula (BLP) model, developed to formalize U.S. military security policy. In the BLP model, a security label is a pair: \((Level, {Compartments})\), where \(Level\) is a hierarchical classification (e.g., Unclassified, Secret, Top Secret) and \({Compartments}\) is a set of non-hierarchical categories (e.g., NATO, CRYPTO).
The can-flow relation \(≤\) is defined as follows:
Label \(L_1=(Level_1,Compartments_1)\) can flow to Label \(L_2=(Level_2,Compartments_2)\), written \(L1≤L2\), if and only if \(Level_1≤Level_2\) and \(Compartments_1⊆Compartments_2\).
This single rule gives rise to the two famous axioms of the BLP model:
-
The Simple Security Property ("No Read Up"): A subject \(S\) can read an object \(O\) only if the subject’s label dominates the object’s label, i.e., \(Label(O)≤Label(S)\). This ensures that information can only flow from the object to a subject with an equal or higher clearance. -
The \*-Property ("No Write Down"): A subject \(S\) can write to an object \(O\) only if the object’s label dominates the subject’s, i.e., \(Label(S)≤Label(O)\). This ensures information flows from the subject to the object, preventing a high-clearance subject from leaking information into a low-clearance container.
With this formal model, we can now resolve Alice’s dilemma with mathematical precision.
-
Alice's Label: \(S_{Alice}=(TopSecret,{CRYPTO,NATO})\) -
Bob's Document Label: \(O_{Bob}=(Secret,{NATO})\)
For Alice to write to Bob’s document, the no write down rule requires that \(S_{Alice}≤O_{Bob}\). Let’s check the conditions:
- Is \(TopSecret ≤ Secret\)?
No. - Is \({CRYPTO, NATO} ⊆ {NATO}\)?
No.
Since both conditions fail, the relation does not hold. The lattice model formally forbids the operation, preventing the information leak. The system doesn’t need to understand the content of the document; it only needs to compare the labels according to the lattice rules.
The following table illustrates how the lattice structure governs access decisions in a BLP system.
| Subject Label (S) | Object Label (O) | Can Read? (\(O \leq S\)) | Can Write? (\(S \leq O\)) | Explanation |
|---|---|---|---|---|
| \((\text{TS}, \{N, C\})\) | \((\text{S}, \{N\})\) | Yes | No | Subject dominates object (higher level, superset of compartments). Read is permitted. |
| \((\text{S}, \{N\})\) | \((\text{TS}, \{N, C\})\) | No | Yes | Object dominates subject. “No read up” is enforced, but “write up” is permitted. |
| \((\text{S}, \{N\})\) | \((\text{S}, \{C\})\) | No | No | Incomparable. Neither label dominates the other due to disjoint compartments (\(\{N\} \nsubseteq \{C\}\) and vice versa). No flow is allowed. |
| \((\text{TS}, \{N, C\})\) | \((\text{TS}, \{N, C\})\) | Yes | Yes | Equal labels. Read and write operations within the same security context are permitted. |
Lattices in Action
Lattice theory isn’t just a beautiful piece of mathematics tucked away in textbooks. It’s the invisible scaffolding behind some of the most secure systems in the digital world. From how your operating system blocks hackers to how modern software prevents data leaks before it even runs, lattices are quietly doing the heavy lifting.
Operating System Security: SELinux
One of the most powerful real-world uses of lattice-based access control is found inside the Linux operating system, specifically in a feature called Security-Enhanced Linux (SELinux). You might never see it, but it’s likely protecting servers that host everything from banks to national defense systems.
Here’s how it works:
- In
SELinux, every process (like a running program) and every file is labeled with a security level, such as Public, Secret, or Top Secret, along with a category like {Finance} or {System}. - These labels are arranged into a lattice, forming a hierarchy of who can access what.
- The system enforces rules like
no read upandno write down, meaning a less privileged process can’t snoop on or overwrite more sensitive data.
Imagine a web server labeled as \((Public, \{\})\). If a hacker takes control of it, they’re still trapped because SELinux, guided by the lattice, won’t let that process read files labeled \((Secret, \{System\})\). The attacker hits an invisible wall they can’t climb. The lattice becomes a mathematical cage, confining even compromised programs within strict boundaries.
Secure Software Development
Preventing leaks after a program runs is good, but what if we could prevent insecure programs from being written at all?
That’s the promise of a powerful security principle called noninterference. It means:
“If someone only has access to public outputs, they should learn nothing about secret inputs, no matter how clever they are.”
Sounds simple, but information leaks can be sneaky. For example:
if (secret_key > 1000) {
public_counter = 1;
} else {
public_counter = 0;
}
There’s no direct leak like \(\text{public_counter = secret_key}\), but just observing the value of \(\text{public_counter}\) reveals information about \(\text{secret_key}\). This is called implicit information flow, and it’s surprisingly hard to catch.
This is where lattices shine again.
In modern security-aware programming languages, every variable is given a security label—again, forming a lattice. The compiler watches how information flows through your code. If a secret value ever influences a public variable (even indirectly) it throws an error before the code is ever run.
This is a big deal. Instead of relying on runtime firewalls to catch bad behavior, we now have a way to prove at compile time that a program is secure. It’s like having a spell checker that catches privacy bugs instead of typos. The same lattice structure that protected operating systems at runtime is now helping us build provably secure software from the start.
What’s profound here is the shift in mindset:
-
Traditional security says: “Run the program, then try to stop it from doing bad things.” -
Lattice-based security says: “Let’s make sure the program can’t do bad things—even if it tries.”
The lattice is the common thread tying these two worlds together: a bridge between theory and practice, between enforcement and design. It quietly powers a new generation of systems where trust isn’t an assumption, it’s a guarantee.
The Final Verdict
Our journey began with a spy’s dilemma, a question of control, secrecy, and trust. What started as a simple security constraint led us through the abstract universe of partial orders and lattices, unveiling a hidden geometry of relationships. And from that abstract order, we returned full circle to the very real world of secure operating systems, classified documents, and provably correct software.
What makes this story remarkable is not just its mathematical elegance, but its deep philosophical resonance:
- How do we trust systems we cannot fully observe?
- How do we define boundaries of knowledge in a world where information flows invisibly?
- And who decides who is allowed to know what?
Lattice theory, answers these questions not with rules of thumb but with mathematical inevitability. It replaces ad-hoc permissions and bureaucratic guesswork with a single, predictable structure. In doing so, it offers more than just technical security, it offers epistemological clarity.
In an age where information is both our most valuable asset and our most subtle vulnerability, this clarity is no luxury, it’s essential. The lattice is not just a mathematical construct. It’s an invisible architecture of trust, a formal grammar for governing what can be known, by whom, and when.
But here’s something worth pondering as you leave this page:
- If trust in systems can be built from abstract mathematics… can trust in society be as well?
I’d love to hear your thoughts. Drop your reflections, questions, or alternate interpretations in the comment section below, and don’t forget to leave a quick reaction if this sparked something in you.
Let the conversation continue, because the most interesting part of any theory is what it helps us question next.