Pi vs. AI: Could a Neural Network Predict the Next Digit of Pi?
\(π (pi)\) is a mathematical constant defined as the ratio of a circle’s circumference to its diameter, approximately \(3.14159\). The symbol π was introduced by British mathematician William Jones in 1706 and later popularized by Swiss mathematician Leonhard Euler.
Pi holds a significant place in human history, dating back thousands of years across multiple civilizations:
-
2000 BCE (Babylonians): Approximated \(π ≈ 3.125\) for construction. -
1650 BCE (Egyptians, Rhind Papyrus): Used \(π ≈ 3.16045\) for practical calculations, including pyramid construction. -
\[\frac{223}{71} < \pi < \frac{22}{7}\]250 BCE (Archimedes, Greece): Inscribed and circumscribed polygons up to 96 sides, narrowing \(π\) to: -
Medieval Mathematicians (China, India, Arabia): Extended \(π\)’s decimal places using tedious calculations. -
European Mathematicians (17th Century): Introduced infinite series and later, with calculus, computed \(π\) to hundreds of digits. -
Modern Era: In 2024, researchers computed 202 trillion digits of \(π\), while some individuals have memorized over 100,000 digits.
As we push computational limits to calculate \(π\)’s digits, a fun question arises: Can AI predict the next digits of \(π\)? AI can predict the next word in a sentence, the next frame in a video, and even your next favorite song on Spotify. But what happens when we throw pure mathematics at it? Can AI predict the next digits of \(π\)?
Short Answer: No
But you’re not here just for that right? So let’s dive deeper!
What’s special about pi?
Pi is an irrational number, meaning it cannot be expressed as a ratio of two integers. You might say, “But we write π as 22/7!” that’s just an approximation, not the exact value. In simpler terms, \(π\) is irrational because its decimal expansion never ends and never repeats. No matter how many digits you calculate, you will never find a pattern or a simple fraction that exactly equals \(π\).
For example:
1/2 = 0.5 (stops)
1/3 = 0.333... (doesn’t stop but follows a fixed repeating pattern)
π = 3.14214159265358979... (continues infinitely without any pattern)
Think of \(π\) as a Netflix series that NEVER ENDS and NEVER REPEATS but unfortunately, one that doesn’t exist (yet). But \(π\) isn’t just irrational, it’s also transcendental, meaning it cannot be the solution to any algebraic equation with integer coefficients like \(ax^n + bx^{n-1} + \dots + cx + d = 0\). This makes it even more special!
How special? Special enough that on March 12, 2009, the U.S. Congress officially declared March 14 (3/14) as National Pi Day, a day for math lovers, pie lovers, and those who enjoy an excuse to celebrate a never-ending number.
Though \(π\) seems to be related to circles it pops up in unexpected places: it’s found in physics equations, probability theory, number theory, and even in the fundamental principles of quantum mechanics and chaos theory. It governs the oscillations of a pendulum, the shape of rivers, human DNA, and even the distribution of prime numbers.
Pi isn’t just a number; it’s a mathematical mystery that continues to fascinate and challenge us!
Understanding Randomness vs Patterns
Human brains are wired to recognize structure, complete sentences, and anticipate future events based on past experiences, a tendency known as apophenia in psychology. But does this ability apply to all sequences, including numbers?
Let’s play a quick game:
If I say: “Once upon a…”
→ You expect “time.”
If I give you: 1, 4, 9, 16, 25, ?
→ You’d likely say 36 (each term is the square of the next integer).
But if I give you: 3.1415926535… ?
→ What’s next? No clear rule to predict it!
AI, particularly neural networks, are incredibly good at recognizing patterns because they process vast amounts of data and extract relationships humans might miss. They outperform humans in tasks like speech recognition, image classification, and even detecting hidden trends in stock markets. But what happens when there’s no pattern to learn?
Pi is a prime example of this paradox. While its digits appear random, \(π\) itself is not truly random, it is a deterministic number, meaning every digit is precisely defined by mathematical computation. If you start calculating π using an algorithm, you will always get the same sequence of digits. There’s no uncertainty or chance involved in generating \(π\)’s digits; they follow from well-established formulas like the Leibniz series, the Chudnovsky algorithm, or the BBP formula, which can compute any specific digit of \(π\) without needing to calculate the preceding ones.
However, despite being deterministic, \(π\) exhibits statistical randomness in its decimal expansion. This means that while each digit is uniquely determined, the sequence lacks any repeating pattern or simple formula that can predict future digits without performing calculations. For example, if you analyze the frequency of digits in a sufficiently large stretch of \(π\), you’ll find that each digit (0–9) appears roughly equally often, similar to how random numbers behave in probability theory. This suggests that \(π\) might be a normal number, meaning its digits are uniformly distributed in every base. Although normality hasn’t been proven for \(π\), extensive computations strongly support it.
To put it another way, imagine flipping a fair coin. While each flip is determined by physical laws, the outcomes over many trials will still form a sequence that appears random, with no discernible pattern. Similarly, AI can analyze millions of \(π\)’s digits, but it won’t find a shortcut to predict the next one because none exists. Unlike language patterns or image structures that AI can learn from past data, \(π\)’s digits do not follow any learnable rule that generalizes beyond computation.
So, what if AI did manage to predict the next digit of \(π\)? That would imply a hidden pattern in \(π\)’s digits, one that no mathematician has ever discovered. But so far, every attempt to find such a pattern has failed.
Experimental Setup
To test whether AI can detect patterns in the digits of \(π\), we trained an LSTM (Long Short-Term Memory) neural network, a type of AI designed for sequence prediction. LSTMs are particularly effective for sequential data because they can retain information over long durations. Think of a standard neural network as someone with short-term memory loss that forgets what happened just a moment ago. In contrast, an LSTM is like someone taking notes, remembering key details to recognize patterns over time.
Since \(π\) is an infinite sequence of digits, an LSTM should, in theory, be able to detect any hidden patterns if they exist.
PI Model
For our experiment, we trained an LSTM model using 100,000 digits of \(π\) as input. The model was trained for 10 epochs, during which we recorded the loss, confidence, and accuracy at each stage. We used the cross-entropy loss function, which is commonly applied in classification tasks where the model predicts a probability distribution over multiple possible outcome (digits 0–9).
On average, the model’s loss was around 2.3027, which suggests that the AI was unable to detect any meaningful structure in the digits of \(π\).
To establish a baseline, we compared our trained AI’s accuracy to random guessing, where each digit (0–9) has an equal probability of appearing. If the AI discovered a pattern, its accuracy should surpass accuracy of random guessing. If not, it would confirm that \(π\)’s digits are truly unpredictable.
Hypothesis
- If AI finds a pattern, accuracy should exceed 10% (better than random guessing).
- If AI fails, it means \(π\)’s digits behave like a statistically random sequence.
Fibonacci Model
To demonstrate that AI is indeed capable of learning patterns in numerical sequences, we trained the exact same LSTM model on the Fibonacci sequence instead of \(π\). However, since Fibonacci numbers grew exponentially, we focused on their last digits (MOD 10) rather than their full values.
A fascinating property of Fibonacci MOD 10 is that it follows a repeating cycle every 60 terms:
Fibonacci MOD 10 Cycle (Every 60 Numbers)
0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4,
1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7,
9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7,
2, 9, 1, → 0, 1, 1, 2, 3, 5, 8, ... (repeats every 60 terms!)
We again recorded the epoch, loss, confidence, and accuracy of the AI model during training. We used cross-entropy loss here as well. Unlike the \(π\) model, this time the loss was approximately 0.003, indicating the model successfully learned the sequence.
Hypothesis
- Since the Fibonacci sequence has a clear pattern, AI should achieve close to 100% accuracy in predicting the next digit.
The Result
After training our AI models on both \(π\) and Fibonacci sequences, the results were crystal clear \(π\) remained unpredictable, while Fibonacci was effortlessly learned by the AI. These findings directly validate our initial hypothesis.
Pi Model
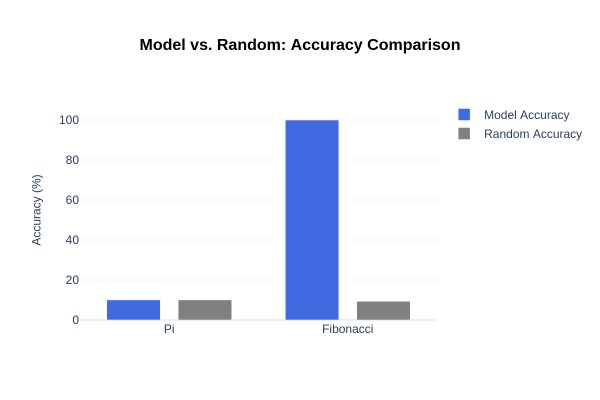
In our hypothesis, we stated that if AI could detect a pattern in \(π\), its accuracy should exceed 10% otherwise, \(π\) is truly unpredictable. Our model failed to exceed 10% accuracy, which is exactly what we’d expect from random guessing. No matter how many digits it processed, the model never improved it was essentially guessing blindly.
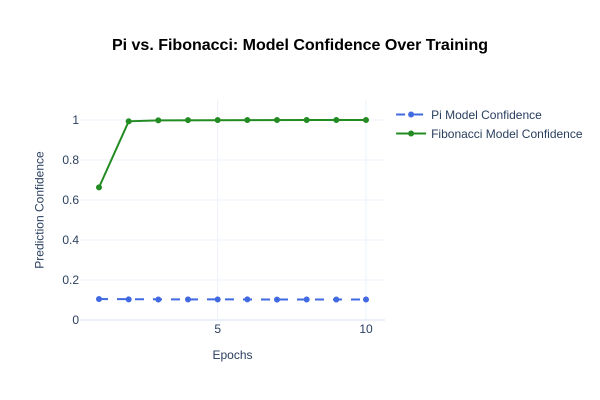
Even more telling was its low confidence (~0.10) throughout training. Normally, as AI learns a pattern, its confidence increases, but with \(π\), the model never became “sure” of its predictions. This result reinforces what mathematicians have long suspected \(π\)’s digits are statistically random. If a hidden pattern existed, our AI should have picked up on it, but it didn’t.
Thus, the π model confirmed our hypothesis: \(π\) behaves like a truly random sequence.
Fibonacci Model
In contrast, our second hypothesis stated that if a sequence has an underlying pattern, AI should detect it and achieve near-perfect accuracy.
This time our results were striking. The Fibonacci model quickly achieved nearly 100% accuracy, proving that it successfully learned the repeating cycle. Unlike the π model, where confidence stayed low, the Fibonacci model started at 66% confidence in the first epoch and soared to nearly 100% confidence within a few epochs, where it remained.
This directly validated our hypothesis that when a sequence follows a clear mathematical rule, AI can learn it almost instantly.
Following graphs capture the results of our experiment:
This implies that \(π\) remains as mysterious as ever, and no AI is going to crack it anytime soon.
If you want to replicate this experiment, you can find the code and instructions here.
What does this mean for AI?
This naturally raises a question: What if we used a deeper neural network or trained on a much larger dataset say, millions or even billions of digits of \(π\)? Would that improve the results? The short answer is no, and here’s why. The limitation isn’t in the model’s complexity or the amount of data it’s in the nature of \(π\) itself. Unlike language, stock prices, or even the Fibonacci sequence, where patterns exist but may be difficult to detect, \(π\)’s digits have no underlying rule that can be learned. No matter how deep the neural network is or how much data it trains on, it can’t learn something that doesn’t exist.
We can make this argument even stronger by comparing it directly to the Fibonacci model. Both models were trained on the exact same dataset size 100,000 digits yet the Fibonacci model achieved nearly perfect accuracy, while the \(π\) model remained stuck at random guessing. This is a crucial point. If the issue were simply not enough training data, then the Fibonacci model should have also struggled but it didn’t. The AI had more than enough data to learn the repeating Fibonacci cycle, proving that when a pattern exists, the AI can find it. The failure of the \(π\) model wasn’t due to dataset size or model complexity, it was because no pattern exists to be learned.
The Final Verdict
After all the training, testing, and number crunching, one thing is clear AI is smart, but not a magician. It can learn structures, spot trends, and even beat humans in pattern recognition. But when it comes to \(π\), AI is just as lost as the rest of us. No matter how deep the neural network or how many digits we feed it, \(π\) remains an unsolvable enigma an infinite, pattern less sequence that defies prediction.
But let’s take a moment to imagine, what if AI did predict \(π\)? What if, instead of random guessing, it started churning out correct digits with eerie precision? That would be earth-shattering. It would mean that \(π\) isn’t truly random, that some hidden pattern governs its digits, and that math itself might be secretly deterministic. Could it be that the universe has a hidden order, a cosmic structure waiting to be uncovered? That’s a question that would send shockwaves through mathematics, physics, and even philosophy.
But, luckily for mathematicians (and unlucky for AI), \(π\) refuses to be cracked. The digits keep flowing, unpredictable as ever, and the universe keeps its secrets for now. So, the next time you see someone trying to train AI on \(π\), just sit back, grab some pie, and enjoy the show. Because if math did turn out to be secretly deterministic, we might just have to rewrite the laws of reality.